Octonion
From Wikipedia, the free encyclopedia
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O orblackboard bold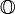 
. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H. The octonions are the largest such algebra, with eight dimensions, double the number of the quaternions from which they are an extension. They arenoncommutative and nonassociative, but satisfy a weaker form of associativity, namely they arealternative.
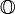. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H. The octonions are the largest such algebra, with eight dimensions, double the number of the quaternions from which they are an extension. They arenoncommutative and nonassociative, but satisfy a weaker form of associativity, namely they arealternative.
Octonions are not as well known as the quaternions and complex numbers, which are much more widely studied and used. Despite this they have some interesting properties and are related to a number of exceptional structures in mathematics, among them the exceptional Lie groups. Additionally, octonions have applications in fields such as string theory,special relativity, and quantum logic.
The octonions were discovered in 1843 by John T. Graves, inspired by his friend William Hamilton's discovery of quaternions. Graves called his discoveryoctaves. They were discovered independently byArthur Cayley[1] and are sometimes referred to asCayley numbers or the Cayley algebra.
No hay comentarios:
Publicar un comentario
ciencia global al cuadrado...